Question

A gas under a pressure of 74 mmHg and at a temperature of 75°C occupies a 500.0-L container. How many moles of gas are in the container?

Answer 1

Answer : The number of moles of gas present in container are 1.697 mole.

Explanation :

Using ideal gas equation,

`PV=nRT`

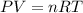
where,

P = pressure of gas = 74 mmHg = 0.097 atm

conversion used : (1 atm = 760 mmHg)

V = volume of gas = 500.0 L

T = temperature of gas =
`75^oC=75+273=348K`

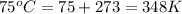
n = number of moles of gas = ?

R = gas constant = 0.0821 L.atm/mole.K

Now put all the given values in the ideal gas equation, we get the number of moles of gas in the container.

`(0.097atm)* (500.0L)=n* (0.0821L.atm/mole.K)* (348K)`

`n=1.697mole`

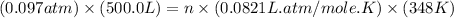
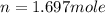
Therefore, the number of moles of gas present in container are 1.697 mole.