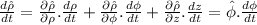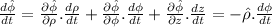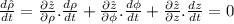Answer:
Provided that the cylindrical coordinate system is given by the coordinates
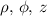
The unit vectors are:
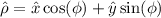
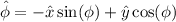

With their time derivatives being:
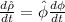
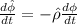
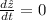
Step-by-step explanation:
Let's start by writing the coordinate transformations:
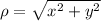 ,
,

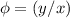 ,
,
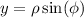
 .
.
For the unit vector
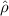 we have:
we have:
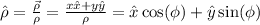
For the unit vector
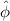 we have:
we have:
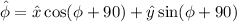
By adding 90 degrees to
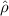 , we have (see the 2nd attachment),
, we have (see the 2nd attachment),
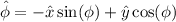
It is not hard to see that
 .
.
From this we can write the following useful expressions that we'll use later on to determine the time derivatives:
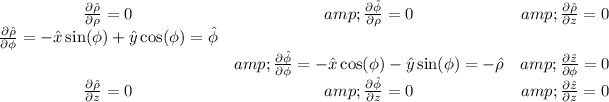
Now, knowing all of the above the time derivatives come in a straightforward way: