Question

asked Dec 19, 2020 101k views

2 Answers

Colin Cline · Answer 1 · 2020-12-21T22:48:19+0000

Answer:

percentage left = 10 %

241 000 years

Step-by-step explanation:

The half life,
$t_{(1)/(2) }$ of plutonium-239 is 24 100 years.

Thus, the number of half lives that result in the decrease of the nucleotide is given by the following equation:

The percentage left will be 10 %

if
$t_{(1)/(2) } = 24 100$ , then after 10 half-life, the decay will be:

$t_(10 years) = 24 100* 10\\ = 241 000$

JeremyD · Answer 2 · 2020-12-23T20:47:28+0000

Answer:

Step-by-step explanation:

The equation for radioactive decay its:

$N ( t) \ = \ N_0 \ e^{ \ -  (t)/(\tau)}$ ,

where N(t) its quantity of material at time t,
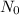N_0 its the initial quantity of material and
$\tau$ its the mean lifetime of the radioactive element.

The half-life
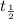$t_{(1)/(2)}$ its the time at which the quantity of material its the half of the initial value, so, we can find:

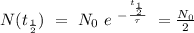
$N (t_{(1)/(2) }) \ = \ N_0 \ e^{ \ -  \frac{t_{(1)/(2)}}{\tau}} \ = (N_0)/(2)$

so:

$\ N_0 \ e^{ \ -  \frac{t_{(1)/(2)}}{\tau}} \ = (N_0)/(2)$

$e^{ \ -  \frac{t_{(1)/(2)}}{\tau}} \ = (1)/(2)$

$-  \frac{t_{(1)/(2)}}{\tau}} \ = - \ ln( 2 )$

$t_{(1)/(2)}\ = \tau ln( 2 )$

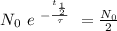
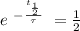
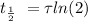
So, after 10 half-lives, we got:

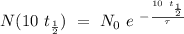
$N ( 10 \  t_{(1)/(2)}) \ = \ N_0 \ e^{ \ -  \frac{10 \  t_{(1)/(2)}}{\tau}}$

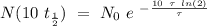
$N ( 10 \  t_{(1)/(2)}) \ = \ N_0 \ e^{ \ -  (10 \  \tau \ ln( 2 ) )/(\tau)}$

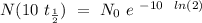
$N ( 10 \  t_{(1)/(2)}) \ = \ N_0 \ e^( \ -  10 \  \ ln( 2 ) )$

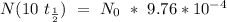
$N ( 10 \  t_{(1)/(2)}) \ = \ N_0 \ * \ 9.76 * 10^(-4)$

So, we got that a 0.09 % of the original radioactive nucllde its left.

Putonioum-239 has a half-life of 24,110 years. So, 10 half-life will take to pass

$10 \ * \ 24,110 \ years \ = \ 241,100 \ years$

It will take 241,100 years for 10 half-lives of plutonium-239 to pass.

Please log in or register to add a comment.