Question

Arithmetic sequences et sn} be an arithmetic sequence that starts with an initial index of 0. The initial term is 3 and the common difference is -2. What is sz? (b) Consider the arithmetic sequence: 7, 4, 1, ... What is the next term in the sequence?

Answer 1

(a) The value of
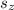`s_z` is (z+1)(3-z).

(b) The next term in the sequence is -2.

Explanation:

(a)

It is given that arithmetic sequence that starts with an initial index of 0.

The initial term is 3 and the common difference is -2.

`a_0=3`

`d=-2`

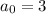
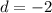
We need to find the value of
`s_z`.

`s_z=\sum_(n=0)^(n=z)(a+nd)`

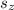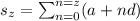
where, a is initial term and d is common difference.

`s_z=\sum_(n=0)^(n=z)(3-2n)`

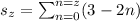
The sum of an arithmetic sequence with initial index 0 is

`s_n=(n+1)/(2)[2a+nd]`

where, a is initial term and d is common difference.

Substitute n=z, a=3 and d=-2 in the above formula.

`s_z=(z+1)/(2)[2(3)+z(-2)]`

`s_z=(z+1)/(2)[2(3-z)]`

`s_z=(z+1)(3-z)`

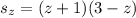
Therefore the value of
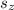`s_z` is (z+1)(3-z).

(b)

The given arithmetic sequence is

7, 4, 1, ...

We need to find the term in the sequence.

In the given arithmetic sequence the first term is

`a=7`

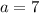
The common difference of the sequence is

`d=a_2-a_1\Rightarrow 4-7=-3`

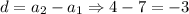
The first term is 7 and common difference is -3.

Add common difference in last given term, i.e., 1, to find the next term of the sequence.

`1+(-3)=1-3=-2`

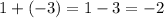
Therefore the next term in the sequence is -2.