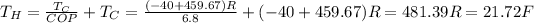Question

"A reversible refrigeration cycle operates between cold and hot reservoirs at temperatures TC and TH, respectively.

(a) If the coefficient of performance is 6.8 and TC = -40°F, determine TH, in °F.
(b) If TC = -15°C and TH = 30°C, determine the coefficient of performance.
(c) If QC = 500 Btu, QH = 600 Btu, and TC = 20°F, determine TH, in °F.
(d) If TC = 10°F and TH = 100°F, determine the coefficient of performance.
(e) If the coefficient of performance is 2 and TC = -5°C, find TH, in °C.
If the coefficient of performance is 6.8 and TC = -40°F, determine TH, in °F. g?"

Answer 1

Explanation:

In order to answer all this questions, you need to know that the the coefficient of performance is the amount of heat removed by the system divided by the work required by the system. Using first law of thermodynamics, the work W can be calculated with the expression
`Q_H-Q_C`, where
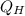`Q_H` is the heat transferred by the hot reservoir and
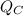`Q_C` the heat collected by the cold reservoir. Then, the expression to calculate the coefficient of performance of a refrigeration cycle would be:

`COP_(refrig)=(Q_C)/(Q_H - Q_C) =(T_c)/(T_H-T_c)`

Important: The temperatures must be in absolute units (Rankine or Kelvin)

a)
`T_H = (T_C + T_C*COP)/(COP) = ((-40+459.67)R + (-40+459.67)R*6.8)/(6.8)=481.386 R - 459.67 = 21.72°F`

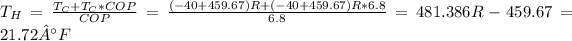
b)
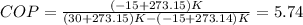
`COP = ((-15+273.15)K)/((30+273.15)K -(-15+273.14)K ) = 5.74`

c)
`(Q_C)/(Q_H - Q_C) =(T_c)/(T_H-T_c)`

`T_H=  T_C*(Q_H - Q_C)/(Q_C) + T_C = (20 +459.67)R * (600 Btu - 500Btu)/(500 Btu) + (20 +459.67)R  = 575.604 R = 115.934 F`

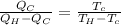
d)
`COP = (T_c)/(T_H-T_c) = ((10+459.67)F)/((100+459.67)-(10+459.67)) = 5.22`

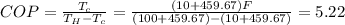
e)
`T_H = (T_C)/(COP) + T_C =  ((-5 + 273.15)K)/(2) +  (-5 + 273.15)K = 402.225K = 129.075 C`

f)
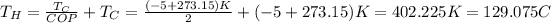
`T_H = (T_C)/(COP) + T_C =  ((-40 + 459.67)R)/(6.8) +  (-40 + 459.67)R = 481.39R = 21.72 F`