Answer:
Part 1) The fractions in the list are not equal to the decimal number indicated
Part 2) The fractions 401/99 and 802/198 are equal to the decimal number indicated.
Explanation:
Part 1)
we have the decimal number
4.05 -----> is a terminating decimal ( t's a decimal with a finite number of digits)
Convert to fraction number
Multiply and divide by 100
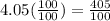
Simplify
Divide by 5 both numerator and denominator

therefore
The fractions in the list are not equal to the decimal number indicated.
Part 2) we have
4.050505... ------> is a repeating decimal (is a decimal that has a digit, or a block of digits, that repeat without ever ending)
Let
x=4.050505...
we have that

Multiply by 2 both numerator and denominator
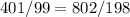
therefore
The fractions 401/99 and 802/198 are equal to the decimal number indicated.