Answer:
Option C
y=5x-11
Explanation:
We first find the gradient,m, of the line that passes through the points (3,4) and (2,-1)
Let
x=3
y=4
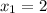
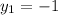
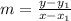
By substitution,

Putting that m=5, x=3 and y=4 into the general equation,
y=mx+c
This implies that
4=5(3)+c
4=15+c
4-15=c
c=-11
The equation of the line is given as
y=mx+c
where m=5 and c=-11
Hence y=5x-11