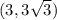Answer:
Check below for multiple forms of the two vectors
Explanation:
So assuming all interior angles are equal.
This means, the interior angles, are 60, 60, 60.
So we're calculating the vector of BA, and BC.
The thing with BC, is that the angle is really zero degrees, since it's just a straight line, that is going to the right. This is really important to note, since a straight line can be 0 degrees, or 180 degrees.
The BA vector however is at an angle of 60 degrees, which was mentioned before as to why.
We can use the trigonometric form of vectors which expresses it as:

where ||v|| = magnitude, and the theta is the just the angle of the vector.
It's convenient to express it in this form, in our case and the reason for this, is that we know the magnitude, and the direction or angle.
So let's start with the BC vector, which as mentioned before has an angle of zero:
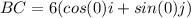
In this trigonometric form, we can convert it to component/linear form since we can easily calculate cos(0) and sin(0) using either a calculator or the unit circle:
So calculating these values we get:
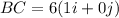
Distributing out the 6 you get:

We can also express this in component form as:
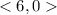
This representation makes sense, since from B to C, you're going to the right so the "i" component which is really just the "x" value, is going to the right 6 which is the magnitude, and the "j" component which is really just the "y" value, is not changing at all.
Now let's do the same thing with BA
We know the angle is 60, and the magnitude is 6
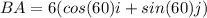
So it might be a bit more convenient to leave it in this form, since sin(60) doesn't evaluate to a rational number, but if you were to convert it to linear form, you can get the exact value using the unit circle
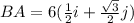
Distributing out the 6 you get:
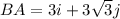
This can also be expressed in component form as: