Question

Using a directrix of y = −3 and a focus of (2, 1), what quadratic function is created?

Answer 1

Answer: a

Explanation:

Answer 2

`y=(1)/(8)(x-2)^2-1`

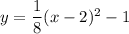
Explanation:

The distance between the focus and the directrix is the vertical distance from the point to the line:

1 -(-3) = 4

The vertex is half that distance between the point and the line, so is at x=2 and ...

y = (-3 +1)/2 = -1

The vertical scale factor of the quadratic is 1/(4p) where p is the distance from vertex to focus. Here, that distance is 2, so the equation in vertex form is ...

y = (1/(4·2))(x -2)² -1

y = (1/8)(x -2)² -1

_____

Check

Any point on the parabola is equidistant from the focus and directrix. This is easily checked at the vertex, which is halfway between focus and directrix, and at the points having the same y-value as the focus. Those two points are (-2, 1) and (6, 1), both of which are 4 units from the focus and 4 units from the directrix.