Question

Can you rewrite a sine as a cosine function and vice versa when describing a general sinusoidal graph? Explain.

Answer 1

`sin(x+(\pi)/(2))=cos(x)`

`cos(x-(\pi)/(2))=sin(x)`

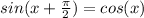
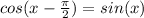
Explanation:

* Lets explain how to solve the problem

- We can write a sine as a cosine by translate the sine function to the

left by
`(\pi)/(2)`

-
`sin(x+(\pi)/(2))=cos(x)`

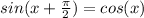
∵ The value of sin(0 + π/2) = 1

∵ cos(0) = 1

∴ sin(0 + π/2) = cos(0)

∴ If sin(x) translated to the left by
`(\pi)/(2)`, then it will be

cos(x)

∴
`sin(x+(\pi)/(2))=cos(x)`

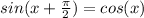
- Vice versa

- We can write a cosine as a sine by translate the cosine function to

the right by
`(\pi)/(2)`

-
`cos(x-(\pi)/(2))=sin(x)`

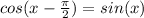
∵ The value of cos(0 - π/2) = 0

∵ sin(0) = 0

∴ cos(0 - π/2) = sin(0)

∴ If cos(x) translated to the right by
`(\pi)/(2)`, then it will be

sin(x)

∴
`cos(x-(\pi)/(2))=sin(x))`

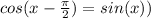
- Look to the attached graphs for more understand