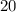Answer:
\\x= P/(c -d)[/tex],
Assume that the price of each minute in the first plan is $c and that the second plan charges a flat rate of $P and a charge of additional $d for every minute.
Explanation
Assume that the price of each minute in the first plan is $c and that the second plan charges a flat rate of $P and a charge of additional $d for every minute.
Thus, the monthly cost of a customer who consumes x minutes in each plan is:
For the first plan:

and for the second plan:
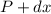
Considering that the monthly costs must be the same in each plan, you have to:
![cx = P + dx\\ transposing terms</p><p>\\cx - dx = P\\ applying common factor</p><p>\\(c -d)x = P\\ dividing by [tex]c - d](https://img.qammunity.org/2020/formulas/mathematics/college/w4351hzie1f6rd7vyyyd9x8hxak1ucqi1x.png)
\\x= P/(c -d)[/tex].
For example if
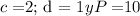 , Then the number of minutes would be,
, Then the number of minutes would be,
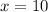 and the total cost for each plan would be
and the total cost for each plan would be