Question

Solve the system of linear equations.


`\displaystyle 3x+5y=27`

`\displaystyle 6x+6y=42`

Answer 1

(4, 3)

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtract Property of Equality

Algebra I

• Solving systems of equations using substitution/elimination
• Solving systems of equations by graphing

Explanation:

Step 1: Define Systems

3x + 5y = 27

6x + 6y = 42

Step 2: Rewrite Systems

3x + 5y = 27

1. Multiply everything by -2: -6x - 10y = -54

Step 3: Redefine Systems

-6x - 10y = -54

6x + 6y = 42

Step 4: Solve for y

Elimination

1. Combine 2 equations: -4y = -12
2. Divide -4 on both sides: y = 3

Step 5: Solve for x

1. Define equation: 3x + 5y = 27
2. Substitute in y: 3x + 5(3) = 27
3. Multiply: 3x + 15 = 27
4. Subtract 15 on both sides: 3x = 12
5. Divide 3 on both sides: x = 4

Step 6: Graph Systems

Check our solution set (4, 3) to see if it is actually the solution set.

Where the 2 lines intersect is the solution set to the systems of equations.

We see that the graph also has the intersection/solution set of (4, 3).

∴ Point (4, 3) or x = 4, y = 3 is the solution.

Answer 2

The coordinate point at which both lines intersect on a graph is (4, 3).

Explanation:

We are given two equations:

`\displaystyle \left \{ {{3x + 5y = 27} \atop {6x + 6y = 42}} \right.`

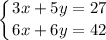
There are three different ways we can solve these equations.

1. Graphing

These equations are currently in standard form, which means they need to be placed in slope-intercept form.

We need to get from:

`\text{Ax + By = C} \rightarrow \text{y = mx + b}`

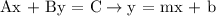
We can see that our equations have the x-variables on the left where they need to be on the right, so we can subtract the x terms from both sides and isolate the y-term.

For equation one:

`\displaystyle 3x + 5y = 27\\\\(3x - 3x) + 5y = 27 - 3x\\\\5y = 27 - 3x \rightarrow 5y = -3x + 27`

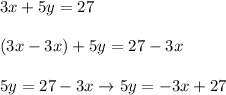
Now, we need to get the y-variable by itself - this requires division. We want to get rid of the coefficient on the y-variable, so we can divide by 5 on both sides of the equation.

`\displaystyle 5y = -3x + 27\\\\(5y)/(5) = -(3x)/(5) + (27)/(5)\\\\y = (3)/(5)x + (27)/(5)`

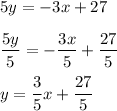
Therefore, we see that our equation is solved in slope-intercept form and can now be plotted on a graph. (Please refer to attachment 1)

In an equation in slope-intercept form, we have two values that are needed to plot the line on the graph.

We need:

1. The y-intercept (b)

2. The slope (m)

Looking at our equation, we know that slope-intercept form is y = mx + b, which means we need to determine what m and b are.

We see that our constant in the solved equation is
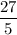`\displaystyle (27)/(5)`, so we know that our y-intercept will occur at 5.4 (the fraction in decimal form) on the y-axis.

We also see that our coefficient to x in our equation is
`\displaystyle (3)/(5)`, which means that our slope is equivalent to this value. This is equal to 0.6 in decimal form.

The slope essentially means that the numerator (3) is the value of units in which the line increases on the graph from the y-intercept. Then, the denominator (5) is how many units the line goes to the right in a straight line from that point.

Therefore, the next point is 3 units up from the y-intercept
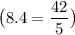`\displaystyle \big(8.4 = (42)/(5)\big)`. Then, the point goes 5 points horizontally to the right, so it will intersect at our new coordinate:
`\displaystyle \big((42)/(5), 5 \big)`.

Then, a straight line can be drawn through these two points.

We can solve the second equation in the same format:

`\displaystyle 6x + 6y = 42\\\\(6x - 6x) + 6y = 42 - 6x\\\\6y = 42 - 6x\\\\6y = -6x + 42\\\\(6y)/(6) = -(6x)/(6) + (42)/(6)\\\\y = -x + 7`

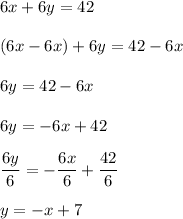
Our equation ends up being y = -x + 7. This can also be plotted on a graph. (Please refer to attachment 2)

We know that our slope is -1 (the -1 is insinuated since we have no value in front of x other than a negative symbol) and that our y-intercept is 7, so we can plot our first point at (0, 7) on the graph. Then, we can descend by one unit to (0, 6) and go to the right by one unit (1, 6). Then, a line can be drawn through the two values.

Now, we need to check to see where our lines intersect. (Please refer to attachment 3)

The lines intersect at one point: (4, 3).

Therefore, the solution to our system of equations is the point (4, 3).