Answer:
B
Explanation:
Let's find perimeter of the 4 circles first.
Each circle is 3/4th of the whole circle. Perimeter of a circle is given by
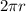 and since we have 3/4th of whole, so the perimeter of one circle would be
and since we have 3/4th of whole, so the perimeter of one circle would be
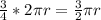
Now, what is the radius?
Since the whole bottom is 915 and the top part is 895 (it excludes 2 radii of 2 circles). So we have 915 - 895 = 20 (20 is equally distributed in 2 radii, so the radius of 1 circle is 20/2 = 10).
Hence, perimeter of 1 circle is
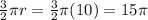
And, 4 of these will have perimeter of

Now, let's find perimeter of the rectangle.
Top and bottom is 895 each, so that's 895 * 2 = 1790
Now, to find the right and left side, we use pythagorean theorem which is
leg^2 + leg^2 = hypotenuse^2
Where two legs are 915 and other one let's call it x, and hypotenuse is 1000-(10+10)=980. Thus,
915^2 + x^2 = 980^2
x^2 = 980^2 - 915^2
x^2 = 123,175
x = Sqrt(123,175)
x = 350.96
x includes the two radius so we need to subtract 10 + 10 = 20, thus we have 350.96 - 20 = 330.96 (left side). So left PLUS right side = 330.96 * 2 = 661.92
Thus, perimeter = 60π + 1790 + 661.92 = 2640.5
B is right.