Question

A bullet of mass 0.02 kg is fired by a gun of mass 20 kg. If the speed of the bullet is 150 ms -1,

calculate the recoil speed of the gun?

Answer 1

0.15m/s

Step-by-step explanation:

Momentum p = mv, must be conserved if there are no external forces acting on the system. Since there are only internal forces acting between the bullet and the gun, momentum must be conserved.

The total momentum before the gun is fired:

`p = m_(bullet)v_(bullet) + m_(gun)v_(gun) = 0.02 * 0 + 20 * 0 = 0`

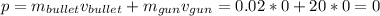
The total momentum after the gun is fired, must also be zero:

`p = m_(bullet)v_(bullet) + m_(gun)v_(gun) = 0.02 * 150 + 20 * v_(gun) = 0`

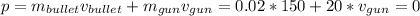
Solving for v:

`v_(gun)=-(m_(bullet)v_(bullet))/(m_(gun)) = -(0.02*150)/(20) =-0.15`

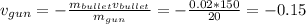
The recoil speed is the absolute value of the velocity.