Answer:
9.
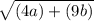 10.
10.
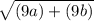 11
11
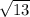
Explanation:
9. Since the Distance Formula is
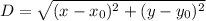
C(a, -b) D(3a, -4b)
Let us plug it in values
D=
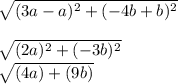
10. C(-a,-2b) D(2a, b)
D=
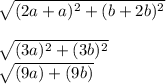
11.
a)AB A(2,3) B(5,5)
D=
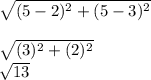
CD C(4,3) D(1,1)
D=
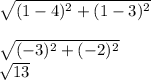
BC B(5,5) C(4,3)
D=
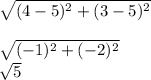
DA D(1,1) A(2,3)
D=
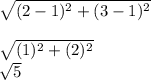
e. The length of each diagonal
AC A(2,3) C(4,3)
D=
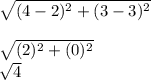
length = 2 u
f.BD B(5,5) D(1,1)
D=
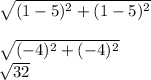 = 4
= 4
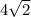
g. No, since congruent diagonals have the same size. Those diagonals do not have congruence between them.
12.
AB A(-2,-1) B(4,1)
D=
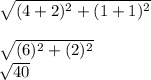 =
=
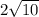
AC A(-2,-1) C(2,-5)
D=
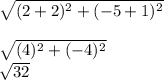 =
=
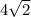
BC B(4,1) C(2,-5)
D=
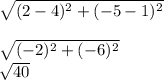 =
=
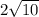
d) AB≅BC