Answer:
a)

b) Proof in explanation.
Explanation:
a)
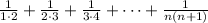 .
.
So let's look at the last term for a minute:
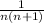
Let's use partial fractions to see if we can find a way to write this so it is more useful to us.

Multiply both sides by
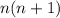 :
:
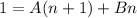
Distribute:

Reorder:
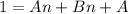
Factor:
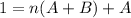
This implies
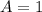 and
and
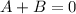 which further implies that
which further implies that
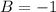 .
.
This means we are saying that:
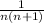 can be written as
can be written as
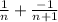
We can check by combing the fractions:
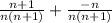
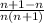
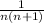
So it does check out.
So let's rewrite our whole expression given to us using this:
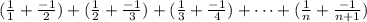
We should see that all the terms in between the first and last are being zeroed out.
That is, this sum is equal to:
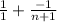
Multiply first fraction by (n+1)/(n+1) so we can combine the fractions:
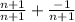
Combine fractions:

b)
Proof:
Let's see what happens when n=1.
Original expression gives us
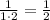 .
.
The expression we came up with gives us
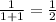 .
.
So it is true for the base case.
Let's assume our expression and the expression given is true for some integer k greater than 1.
We want to now show it is true for integer k+1.
So under our assumption we have:

So let's add the (k+1)th term of the given series on both sides:
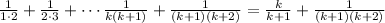
(Now we are just playing with right hand side to see if we can put it in the form our solution which be if we can
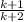 .)
.)
I'm going to find a common denominator which will be (k+1)(k+2):
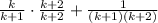
Combine the fractions:
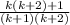
Distribute:
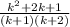
Factor the numerator:
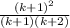
Cancel a common factor of
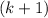
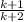
We have proven the given expression and our formula for the sum are equal for all natural numbers,n.