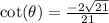Answer:
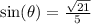
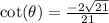
Explanation:
secant and cosine are reciprocal functions.
So if
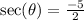 then
then
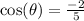 .
.
Now we are going to use Pythagorean Identity:
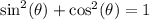 to find the sine value of theta.
to find the sine value of theta.
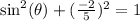
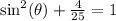
Subtract 4/25 on both sides:
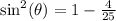
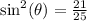
Take the square root of both sides:
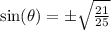
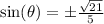
We were given that the cotangent value is negative and that cosine is negative so sine is positive since cotangent is the ratio of cosine to sine.
This means we can rule out the negative value for sine:
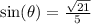
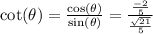
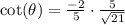
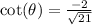
Rationalize the denominator by multiplying numerator & denominator by
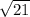 :
: