Answer:
d : 4, 1, -2.
Explanation:
There's no need for a calculator in my opinion because we can use the rational root theorem which states that the equations of this form:
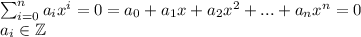
Have rational roots, than the roots are of the form:
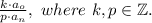
Rewriting the equation we have:

