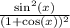Answer:
Proof is in the explanation.
Explanation:
I figure out what you were saying:
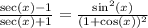
I'm going to try to rewrite left hand side as right hand side.
I'm going to rewrite
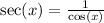 :
:
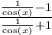
Multiply both numerator and denominator by
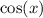 :
:
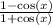
Multiply both numerator and denominator by
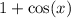 :
:
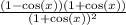
When multiplying conjugates you only have to do first time first and last times last:
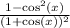
We can rewrite the numerator using the Pythagorean Identity:
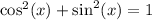 .
.
This gives us: