Question

A, B, and C are collinear, and B is between A and C. The ratio of AB is 1:1. If A is at (1,-9) and B is at (2,0), what are the coordinates of point C

Answer 1

(3,9)

Explanation:

So I drew a right triangle with the line segment A(1,-9) to C
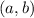`(a,b)` as the hypotenuse. This line segment does contain point B(2,0). This is shown in the picture.

We want to find a point C
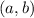`(a,b)` so that AB to BC has a ratio of 1:1. So this means B is the midpoint really.

So if we averaged the endpoints of the line segment it would equate to point B.

That is:

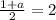`(1+a)/(2)=2` and
`(-9+b)/(2)=0`

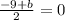
Multiply both sides by 2:

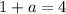`1+a=4` and
`-9+b=0`

The first equation can be solved by subtracting 1 on both sides giving
`a=3`.

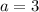The second equation can be solved by adding 9 on both sides giving

`b=9`.

Point C is (3,9).