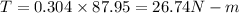Question

A baseball bat could be considered a uniform rod. It ha a mass of 0.97 kg and a length of 97 cm. If a player accelerates it from rest to 2.8 rev/s in 0.20s, how much torque is applied?

Answer 1

The torque is 26.75 N-m.

Step-by-step explanation:

Given that,

Mass = 0.97 kg

Length = 97 cm

Time = 0.20 s

Angular speed
`\omega= 2.8 rev/s = 2.8*2\pi\ rad/s`

We need to calculate the moment of inertia of rod at one end

Using formula of the moment of inertia

`I=(Ml^2)/(3)`

Put the value into the formula

`I=(0.97*(0.97*10^(-2))^2)/(3)`

`I=0.3042\ kg m^2`

We need to calculate the angular acceleration

Using formula of angular acceleration

`\alpha=(\Delta \omega)/(\Delta t)`

Put the value into the formula

`\alpha=(2.8*2\pi)/(0.20)`

`\alpha=87.964\ rad/s^2`

We need to calculate the torque

Using formula of torque

`\tau=I*\alpha`

Put the value into the formula

`\tau=0.3042*87.964`

`\tau=26.75\ N-m`

Hence, The torque is 26.75 N-m.

Answer 2

Applied torque, T = 26.74 N-m

Given:

Mass of rod, M = 0.97 kg

Length of the rod, L = 97 cm = 0.97 m

Change in angular velocity,
`\Delta \omega = 2.8 rev/s = 2.8* 2\pi = 17.59 rad/s`

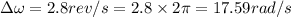
time, t = 0.20 s

Solution:

Now, we know that torque is given by:

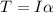`T = I\alpha` (1)

where

I = moment of inertia of the rod

`\alpha` = angular acceleration

Using perpendicular axis formula to calculate the moment of inertia:

`I = (ML^(2))/(12)`

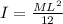
Now, the base ball bat will be held from one end, therefore, the moment of inertia about the axis at the end is given by:

`I = (ML^(2))/(12) + (ML^(2))/(4) = (ML^(2))/(3)`

`I = (0.97* (0.97)^(2))/(3) = 0.304 kg-m^(2)`

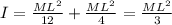
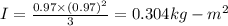
Now, angular acceleration can be calculated as:

`\alpha = (\Delta \omega)/(t) = (17.59)/(0.20) = 87.95 rad/s^(2)`

Now, calculation of torque using eqn (1):

`T = 0.304* 87.95 = 26.74 N-m`