Answer : The correct option is, +91 kJ/mole
Solution :
The balanced cell reaction will be,
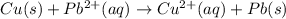
Here copper (Cu) undergoes oxidation by loss of electrons, thus act as anode. Lead (Pb) undergoes reduction by gain of electrons and thus act as cathode.
First we have to calculate the standard electrode potential of the cell.
![E^0_([Pb^(2+)/Pb])=-0.13V](https://img.qammunity.org/2020/formulas/chemistry/high-school/5huqtvusko23g1rdsvievsvmdtdt9y15x0.png)
![E^0_([Cu^(2+)/Cu])=+0.34V](https://img.qammunity.org/2020/formulas/chemistry/high-school/jdqrwlz4jxg7h52em0knt32e6msp300q9m.png)
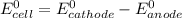
![E^0_(cell)=E^0_([Pb^(2+)/Pb])-E^0_([Cu^(2+)/Cu])](https://img.qammunity.org/2020/formulas/chemistry/college/yj7g1psroztliq56hj2k1hsq5n8wo8j9vc.png)

Now we have to calculate the standard Gibbs free energy.
Formula used :
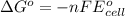
where,
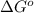 = standard Gibbs free energy = ?
= standard Gibbs free energy = ?
n = number of electrons = 2
F = Faraday constant = 96500 C/mole
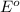 = standard e.m.f of cell = -0.47 V
= standard e.m.f of cell = -0.47 V
Now put all the given values in this formula, we get the Gibbs free energy.
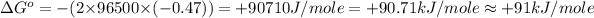
Therefore, the standard Gibbs free energy is +91 kJ/mole