Answer : The mass of
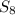 required is 18.238 grams.
required is 18.238 grams.
Explanation : Given,
Mass of
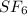 = 83.10 g
= 83.10 g
Molar mass of
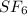 = 146 g/mole
= 146 g/mole
Molar mass of
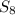 = 256.52 g/mole
= 256.52 g/mole
The balanced chemical reaction is,
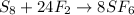
First we have to determine the moles of
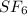 .
.
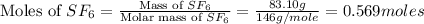
Now we have to determine the moles of
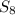 .
.
From the balanced chemical reaction we conclude that,
As, 8 moles of
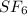 produced from 1 mole of
produced from 1 mole of
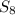
So, 0.569 moles of
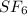 produced from
produced from
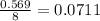 mole of
mole of
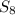
Now we have to determine the mass of
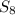 .
.
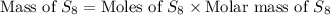
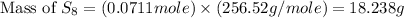
Therefore, the mass of
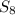 required is 18.238 grams.
required is 18.238 grams.