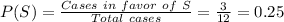Question

A 12-centimeter stick has a mark at each centimeter. By breaking the stick at two of these eleven marks at random, the stick is split into three pieces, each of integer length. What is the probability that the three lengths could be the three side lengths of a triangle?

Answer 1

Answer: The probability that the lengths of the three segments are the side lengths of a triangle is 0.25.

Explanation:

Consider the event "S" as "The three segments are the sides of a triangle." Remember that the probability of an event occurring is calculated according to:

`P(S)=(Cases\ in\ favor\ of\ S)/(Total\ cases)`

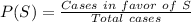
By dividing the stick into three segments, the possible cases that can be obtained writing each case in parenteses and the length of each piece as a number are:

(1, 1, 10), (1, 2, 9), (1, 3, 8), (1, 4, 7), (1, 5, 6), (2, 2, 8), (2 , 3, 7), (2, 4, 6), (2, 5, 5), (3, 3, 6), (3, 4, 5), (4, 4, 4).

which corresponds to a total of 12 total cases.

The necessary condition so that a triangle can be formed is that the sum of its two minor sides is greater than the greater side, therefore the favorable cases would be:

(2, 5, 5), (3, 4, 5), (4, 4, 4)

which corresponds to a total of 3 favorable cases. Using the probability formula we obtain:

`P(S)=(Cases\ in\ favor\ of\ S)/(Total\ cases)=(3)/(12)=0.25`