Question

You drop a batitin a stationary elevator and the ball hits the floor in o 50 s. How long does it take for the ball to hit the floor if the elevator was atready moving up with a constant speed of 1 0 m's when you dropped the ball: Select one a. 0.61 s b. 0.82 s c. 0.41 s d. 0.50 s

Answer 1

Time taken to hit the floor, t = 0.61 s

Option a.

Given:

t = 0.50 s

Solution:

Initial velocity of the ball when dropped, u = 0 m/s

Now, using second equation of motion when acceleration due to gravity acts:

`h = ut + (1)/(2)gt^(2)`

`h = 0 + (1)/(2)* 9.8* 0.5^(2)`

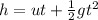
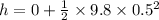
h = 1.225 m

Now, when the lift moves in the upward direction with a constant speed of 1.0 m/s, u = - 1.0 m/s

Time taken by the ball to hit the floor travelling a distance h = 1.225 m is given by:

`h = ut + (1)/(2)gt^(2)`

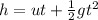
Now,

`1.225 = - 1.0t + (1)/(2)* 9.8* t^(2)`

`4.9t^(2) -t -1.225 = 0`

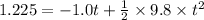
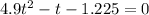
Solving the above quadratic equation, we get:

t = 0.612 s = 0.61 s