Question

A golf ball has a mass of 120g. Calculate its increase in mass when it is travelling at 40ms1. What is this as a percentage of its rest mass?

Answer 1

`Percentage=8.889* 10^(-13)`%

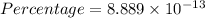Step-by-step explanation:

From special theory of relativity the dynamic mass m is related with the rest mass
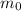`m_(0)`of the body as

`m=\frac{m_(0) }{\sqrt{1-(v^(2) )/(c^(2) ) } }`

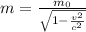
Here, c is the speed of light and v is the velocity of object.

Given mass of the golf ball is 120 g.

`m=\frac{120 }{\sqrt{1-((40)^(2) )/((3* 10^(8) )^(2) ) } }\\m=120(1-((40)^(2) )/((3* 10^(8)) ^(2) ))^{-(1)/(2) } \\`

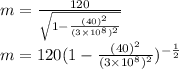
Now applying the binomial theorem and solve the above equation.

`m=(1+(1)/(2)((40)/(3* 10^(8) )) ^(2) )\\m=120(1+8.889* 10^(-15))`

Therefore, increase in mass is,

`\Delta m=120* 8.889* 10^(-15) \\\Delta m=10.6668* 10^(-13) g`

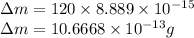
Now percentage of increase in mass with rest mass is,

`Percentage=(10.6668* 10^(-13) g)/(120g) * 100\\Percentage=8.889* 10^(-13)`

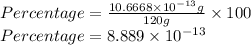
Therefore, the percentage of increase in mass with rest mass is
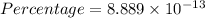`Percentage=8.889* 10^(-13)`.