Question

Particle-X has a speed of 0.720 c and a momentum of 4.350x1019 kgm/s. What is the mass of the particle? 2.0206 10-27 kg Hints: The classical momentum of an object is the product of its mass and its velocity. How does the relativistic momentum look like comp classical momentum? Submit Answer Incorrect. Tries 2/12 PreviouS Tries What is the rest energy of the particle? Submit Answer Tries 0/12 What is the kinetic energy of the particle? Submit Answer Tries 0/12 What is the total energy of the particle?

Answer 1

Step-by-step explanation:

Given that,

Speed of particle = 0.720 c

Momentum = 4.350\times10^{-19}\ kgm/s[/tex]

(I). We need to calculate the mass of the particle

Using formula of momentum

`P=mv`

`m =(P)/(v)`

`m=(4.350*10^(-19))/( 0.720*3*10^(8))`

`m=2.013*10^(-27)\ Kg`

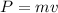
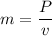
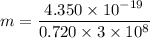
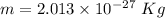
We need to calculate the rest mass of particle

Using formula of rest mass

`m=\frac{m_(0)}{\sqrt{1-((v)/(c))^2}}`

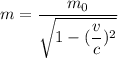
Where,
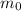`m_(0)` = rest mass

Put the value into the formula

`m_(0)=2.013*10^(-27)*\sqrt{1-((0.720 c)/(c))^2}`

`m_(0)=2.013*10^(-27)*√(1-(0.720)^2)`

`m_(0)=1.4*10^(-27)\ kg`

(b). We need to calculate the rest energy of the particle

Using formula of energy

`E_(0)=m_(0)c^2`

Put the value into the formula

`E_(0)=1.4*10^(-27)*(3*10^(8))^2`

`E_(0)=1.26*10^(-10)\ J`

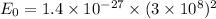
(c). We need to calculate the kinetic energy of the particle

Using formula of kinetic energy

`K.E=mc^2-m_(0)c^2`

`K.E=(m-m_(0))*c^2`

`K.E=(2.013*10^(-27)-1.4*10^(-27))*3*10^(8)`

`K.E=1.84*10^(-19)\ J`

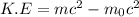
(d). We need to calculate the total energy of the particle

Using formula of energy

`E=mc^2`

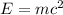
Put the value into the formula

`E=2.013*10^(-27)*(3*10^(8))^2`

`E=1.812*10^(-10)\ J`

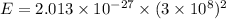
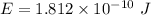
Hence, This is the required solution.