Question

At what net rate does heat radiate from a 300-m^2 black roof on a night when the roof's temperature is 33.0°C and the surrounding temperature is 18.0°C? The emissivity of the roof is 0.900. (Enter the magnitude.)

Answer 1

24445.85 J/s

Step-by-step explanation:

Area, A = 300 m^2

T = 33° C = 33 + 273 = 306 k

To = 18° C = 18 + 273 = 291 k

emissivity, e = 0.9

Use the Stefan's Boltzman law

`E = \sigma  * e * A*\left ( T^4 -T_(0)^(4)\right )`

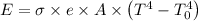
Where, e be the energy radiated per unit time, σ be the Stefan's constant, e be the emissivity, T be the temperature of the body and To be the absolute temperature of surroundings.

The value of Stefan's constant, σ = 5.67 x 10^-8 W/m^2k^4

By substituting the values

`E = 5.64 * 10^(-8)* 0.9 * 300 *  (306^(4)-291^(4))`

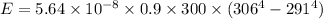
E = 24445.85 J/s