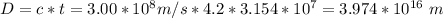Answer:
1.3734 years pass on the astronauts' clock.
The distance measured by astronauts is
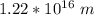
Step-by-step explanation:
The fomula for time dilation is:

where t' is the time observed by the astronauts, t is the time observed form Earth, v is the velocity of the astronaut and c is the velocity of light in a vacuum.
Replacing our values: t=4.2 year, v=0.945c
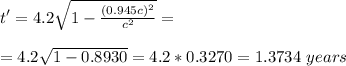
The distance measured by astronauts will be their speed multolied by the time is takes them to get to alpha centauri:
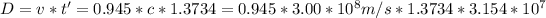
To acomodate fot units we write the speed of light in m/s and the amount of seconds in a year, so the resulting distance will be in meters.
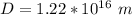
We should compare this to the distance measured from Earth which is