Answer:
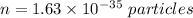
Step-by-step explanation:
It is given that,
Pressure in the intergalactic space,
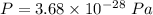
Temperature, T = 2.7 K
Volume,
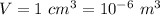
We need to find the number of particles. The formula for the number of molecules in air is given by :
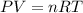 , R is gas constant
, R is gas constant
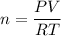
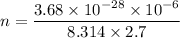
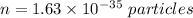
So, the number of particles in intergalactic space is
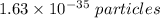 . Hence, this is the required solution.
. Hence, this is the required solution.