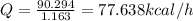Question

A sphere is assumed to have the properties of water and has an initial heat generation 46480 W/m^3 How much should the heat generation term be lowered, if the maximum temperature at the center of the spherical geometry is to be limited to 360 Kelvin? The radius of the sphere is 0.1m ambient air temperature is 25 C. Convert the resulting heat generation to Food Calories per hour

Answer 1

Resulting heat generation, Q = 77.638 kcal/h

Given:

Initial heat generation of the sphere,
`Q_(Gi) = 46480 W/m^(3)`

Maximum temperature,
`T_(m) = 360 K`

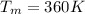
Radius of the sphere, r = 0.1 m

Ambient air temperature,
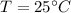`T = 25^(\circ)C` = 298 K

Solution:

Now, maximum heat generation,
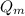`Q_(m)` is given by:

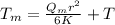`T_(m) = (Q_(m)r^(2))/(6K) + T` (1)

where

K = Thermal conductivity of water at
`T_(m) = 360 K = 0.67 W/m^(\circ)C`

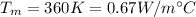
Now, using eqn (1):

`360 = (Q_(m)* 0.1^(2))/(6* 0.67) + 298`

`Q_(m) = 24924 W/m^(3)`

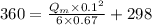
max. heat generation at maintained max. temperature of 360 K is 24924
`W/m^(3)`

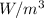
For excess heat generation, Q:

`Q = (Q_(Gi) - Q_(m))* volume of sphere, V`

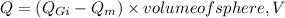
where

`V = (4)/(3)\pi r^(3)`

`Q = (46480 - 24924)* (4)/(3)\pi\0.1^(3) = 21556* (4)/(3)\pi\0.1^(3) W/m^(3)`

`Q = 90.294 W`

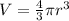
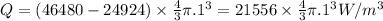
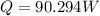
Now, 1 kcal/h = 1.163 W

Therefore,

`Q = (90.294)/(1.163) = 77.638 kcal/h`