Question

Consider a hydrogen atom in the n = 1 state. The atom is placed in a uniform B field of magnitude 2.5 T. Calculate the energy difference between the highest and lowest electronic energy levels in the presence of the B field. a. 9.3 X 10^-5 eV

b. 29 X 10^-5 eV
c. 11.6 X 10^-5 eV

Answer 1

`E=29* 10^(-5)eV`

Step-by-step explanation:

For n-=1 state hydrogen energy level is split into three componets in the presence of external magnetic field. The energies are,

`E^(+)=E+\mu B`,

`E^(-)=E-\mu B`,

`E^(0)=E`

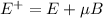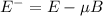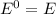
Here, E is the energy in the absence of electric field.

And

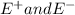`E^(+) and E^(-)` are the highest and the lowest energies.

The difference of these energies

`\Delta E=2\mu B`

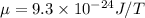`\mu=9.3* 10^(-24)J/T` is known as Bohr's magneton.

B=2.5 T,

Therefore,

`\Delta E=2(9.3* 10^(-24)J/T)* 2.5 T\\\Delta E=46.5* 10^(-24)J`

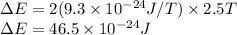
Now,

`Delta E=46.5* 10^(-24)J((1eV)/(1.6* 10^(-9)J ) )\\Delta E=29.05* 10^(-5)eV\\Delta E\simeq29* 10^(-5)eV`

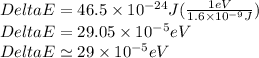
Therefore, the energy difference between highest and lowest energy levels in presence of magnetic field is
`E=29* 10^(-5)eV`