Question

200 cm3 of hydrogen iodide gas (HI) is allowed to dissociate and come to equilibrium. The mixture at equilibrium contained 350 cm3 of gaseous iodine. Calculate K, for the reaction 2HI(g)H(g)+ Ig) (Assume that 1 mol of a gas has a volume of 35 000 cm under the conditions in this experiment.)

Answer 1

Answer : The value of 'K' equilibrium constant is, 0.489

Solution : Given,

Volume of
`HI` =
`200cm^3`

Volume of
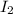`I_2` at equilibrium =
`350cm^3`

Volume of gas for 1 mole of gas =
`35000cm^3`

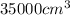
First we have to calculate the moles of
`HI` and
`I_2`.

`\text{Moles of }HI=\frac{Volume of }HI}{\text{Volume for 1 mole of gas}}=(200cm^3)/(35000cm^3)=0.0057mole`

`\text{Moles of }I_2=\frac{Volume of }I_2}{\text{Volume for 1 mole of gas}}=(350cm^3)/(35000cm^3)=0.01mole`

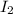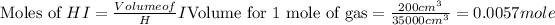
Now we have to calculate the value of equilibrium constant.

The given equilibrium reaction is,

`2HI(g)\rightleftharpoons H_2(g)+I_2(g)`

Initially moles 0.0057 0 0

At equilibrium (0.0057-2x) x x

The expression of
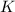`K` will be,

`K=([H_2][I_2])/([HI]^2)`

Let the total volume be 'V'.

`K=(((x)/(V))* ((x)/(V)))/(((0.0057-2x)/(V))^2)`

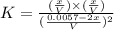
As per question,

Moles of
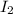`I_2` at equilibrium = x = 0.01

Now put the values of 'x' in the above expression, we get:

`K=(((0.01)/(V))* ((0.01)/(V)))/(((0.0057-2* 0.01)/(V))^2)`

`K=0.489`

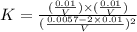
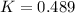
Therefore, the value of 'K' equilibrium constant is, 0.489