Question

A solenoid with 625 loops, each with area 4.34*10^-4 m^2, is originally parallel to a 0.225 T magnetic field. In 0.166 s, it is rotated until it is perpendicular to the field. How much EMF is generated? (Unit Volts)

Answer 1

Answer: -0.368

Step-by-step explanation:

I = BAcos

I(1) = (.225) (4.34*10^-4) cos 0= 9.77*10^-5

I(2)= (.225) (4.34*10^-4) cos 90= 0

E = N • I(2) - I(1) / t

= ((625)(0-9.77*10^-5))/(.166)

= -0.3678 ~ -0.368

Answer 2

EMF, E = 0.061 volts

Step-by-step explanation:

It is given that,

Number of loops in a solenoid, N = 625

Area of the loop,
`A=4.34* 10^(-4)\ m^2`

Magnetic field, B = 0.225 T

It is rotated until it is perpendicular to the field for 0.166 seconds. We need to find the EMF generated in the solenoid. The induced emf is given by :

`E=(-d\phi)/(dt)`

`E=(-d(NBA\ cos\theta))/(dt)`

`E=NBA\ sin\theta`

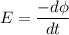
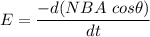
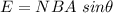
When the solenoid is parallel,
`\theta=0`, E = 0

When the solenoid is perpendicular to the field, E = NBA

`\theta=90`

`E=N* B* A`

`E=625* 0.225* 4.34* 10^(-4)`

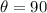
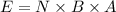
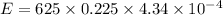
E = 0.061 volts

So, the generated EMF is 0.061 volts. Hence, this is the required solution.