Answer:
A) phase angle = 0.82 rad
B) power factor = 0.68
C) Z = 244 + 264j
D) V(rms) = 162.5 V
E) Pr = 50 W
F) Qc = 11 VA
G) Ql = 65 VA
Step-by-step explanation:
The impedance is:
R + X*j
The reactance is:
X = Xl - Xc
The inductive reactance is:
Xl = w * L = 2π * f * L = 2π * 410 * 0.123 = 317
The capacitive reactance is:
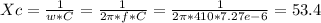
So
X = 317 - 53.4 = 264
Z = 244 + 264j
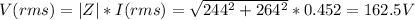
The phase angle is in the first quadrant, it is between 0 and π/2
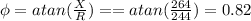
The power factor is the cosine of the phase angle:
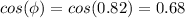
The power consumed by the resistor will be the resistance multiplied by the current(rms) squared
Pr = 244 * 0.452^2 = 50 W
Similar for the capacitor and inductor but with reactance instead of resistance
Qc = 53.4 * 0.452^2 = 11 VA
Ql = 317 * 0.452^2 = 65 VA