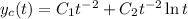Question

Solve the initial value problem 2ty" + 10ty' + 8y = 0, for t > 0, y(1) = 1, y'(1) = 0.

Answer 1

I think you meant to write

`2t^2y''+10ty'+8y=0`

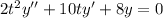
which is an ODE of Cauchy-Euler type. Let
`y=t^m`. Then

`y'=mt^(m-1)`

`y''=m(m-1)t^(m-2)`

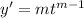
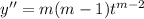
Substituting
`y` and its derivatives into the ODE gives

`2m(m-1)t^m+10mt^m+8t^m=0`

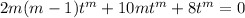
Divide through by
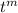`t^m`, which we can do because
`t\\eq0`:

`2m(m-1)+10m+8=2m^2+8m+8=2(m+2)^2=0\implies m=-2`

Since this root has multiplicity 2, we get the characteristic solution

`y_c=C_1t^(-2)+C_2t^(-2)\ln t`

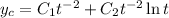
If you're not sure where the logarithm comes from, scroll to the bottom for a bit more in-depth explanation.

With the given initial values, we find

`y(1)=1\implies1=C_1`

`y'(1)=0\implies0=-2C_1+C_2\implies C_2=2`

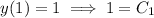
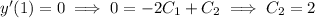
so that the particular solution is

`\boxed{y(t)=t^(-2)+2t^(-2)\ln t}`

# # #

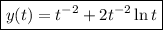
Under the hood, we're actually substituting
`t=e^u`, so that
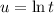`u=\ln t`. When we do this, we need to account for the derivative of
`y` wrt the new variable
`u`. By the chain rule,

`(\mathrm dy)/(\mathrm dt)=(\mathrm dy)/(\mathrm du)(\mathrm du)/(\mathrm dt)=\frac1t(\mathrm dy)/(\mathrm du)`

Since
`(\mathrm dy)/(\mathrm dt)` is a function of
`t`, we can treat
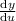`(\mathrm dy)/(\mathrm du)` in the same way, so denote this by
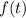`f(t)`. By the quotient rule,

`(\mathrm d^2y)/(\mathrm dt^2)=(\mathrm d)/(\mathrm dt)\left[\frac ft\right]=(t(\mathrm df)/(\mathrm dt)-f)/(t^2)`

and by the chain rule,

`(\mathrm df)/(\mathrm dt)=(\mathrm df)/(\mathrm du)(\mathrm du)/(\mathrm dt)=\frac1t(\mathrm df)/(\mathrm du)`

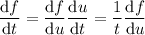
where

`(\mathrm df)/(\mathrm du)=(\mathrm d)/(\mathrm du)\left[(\mathrm dy)/(\mathrm du)\right]=(\mathrm d^2y)/(\mathrm du^2)`

so that

`(\mathrm d^2y)/(\mathrm dt^2)=((\mathrm d^2y)/(\mathrm du^2)-(\mathrm dy)/(\mathrm du))/(t^2)=\frac1{t^2}\left((\mathrm d^2y)/(\mathrm du^2)-(\mathrm dy)/(\mathrm du)\right)`

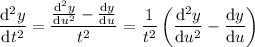
Plug all this into the original ODE to get a new one that is linear in
`u` with constant coefficients:

`2t^2\left(((\mathrm d^2y)/(\mathrm du^2)-(\mathrm d y)/(\mathrm du))/(t^2)\right)+10t\left(\frac{(\mathrm dy)/(\mathrm du)}t\right)+8y=0`

`2y''+8y'+8y=0`

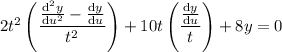
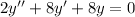
which has characteristic equation

`2r^2+8r+8=2(r+2)^2=0`

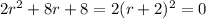
and admits the characteristic solution

`y_c(u)=C_1e^(-2u)+C_2ue^(-2u)`

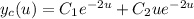
Finally replace
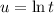`u=\ln t` to get the solution we found earlier,

`y_c(t)=C_1t^(-2)+C_2t^(-2)\ln t`