Question

Use the functions f(x) and g(x) to determine which function has the smallest zero and provide its coordinates.

f(x) = 3x2 + 18x − 21


x g(x)
18 −17
19 0
20 19
21 40
22 63
g(x); (19, 0)
g(x); (−17, 0)
f(x); (−7, 0)
f(x); (1, 0)

Answer 1

The smallest zero is (-7,0) and correspond to f(x)

Explanation:

x g(x) difference of g(x) difference of differences

18 −17

19 0 0 - (-17) = 17

20 19 19 - 0 = 19 19 - 17 = 2

21 40 40 - 19 =21 21 - 19 = 2

22 63 63 - 40 =23 23 - 21 = 2

Then, g(x) is a quadratic function. The regression gives: g(x) = x^2 - 20x +19 (I made it in Excel, you can use any similar software or a calculator).

Using the quadratic formula, the zeros of g(x) are:

`x = (20 \pm √((-20)^2 - 4(1)(19)))/(2(1))`

`x = (20 \pm 18)/(2)`

`x_1 = (20 + 18)/(2)`

`x_1 = 19`

`x_2 = (20 - 18)/(2)`

`x_2 = 1`

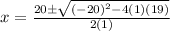
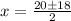
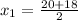
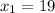
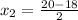
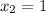
Coordinate of the zeros: (19, 0) and (1,0)

Using the quadratic formula, the zeros of f(x) are:

`x = (-18 \pm √(18^2 - 4(3)(-21)))/(2(3))`

`x = (-18 \pm 24)/(6)`

`x_1 = (-18 + 24)/(6)`

`x_1 = 1`

`x_2 = (-18 - 24)/(6)`

`x_2 = -7`

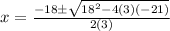
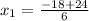
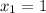
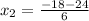
Coordinate of the zeros: (-7, 0) and (1,0)

Answer 2

`f(x); (-7, 0)`

Explanation:

The zeros of a function are those values where the graph of the function touches the x-axis. First, we have
`f(x)` which is a parabola defined by the following equation:

`f(x)=3x^2+18x-21`

By using the quadratic formula, we can get the zeros, therefore:

`x=(-b\pm √(b^2-4ac))/(2a) \\ \\ a=3, \ b=18, \ c=-21 \\ \\ \\ x=(-18\pm √((18)^2-4(3)(-21)))/(2(3)) \\ \\ x=(-18\pm √(324+252))/(6) \\ \\ x_(1)=1 \ and \ x_(2)=-7`

So the zeros of
`f(x)` are
`x_(1)=1 \ and \ x_(2)=-7`. The zero of
`g(x)` is just one and can be determined from the table, which is
`x=19`. So we can see that
`f(x)` is the function that has the smallest zero, which is:

`\boxed{f(x); \ (-7, 0)}`