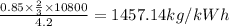Answer:
1.
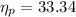
2.
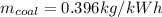
3. carbon emission = 0.297 kg/kWh[/tex]
4. carbon-dioxide emission = 1.089 kg/kWh
5. Min flow of cooling water = = 1457.14 kg/kWh
Given:
Heat Rate = 10,800 kJ/kWh
Heating value = 27,300 kJ/kg
Solution:
In order to calculate the plant efficiency, [rex]\eta_{p}[/tex]
Heat rate in coal fired steam power plant =
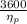
Therefore,
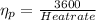
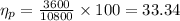
Now,
To calculate mass of coal per kWh,
 :
:


Now,
Rate of emission carbon and carbon-dioxide from the plant:
In accordance to the question, 75% of the bituminous coal being burned is carbon, thus carbon emission is given by:
carbon emission =
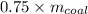
carbon emission =
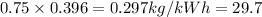
Now, for carbon-dioxide emission:
Since, molecular weight of carbon-dioxide = 44 kg
Thus carbon-dioxide emission:
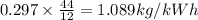
The minimum flow of cooling water per kWh if the allowance in temperature is
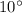 :
: