Question

For the function f(x) = sin(3x) + x^2 + 5, a. Demonstrate that this relationship is non-linear. (Check both requirements) b. Linearise the relationship about an operating point of Xo = 1.2 rad.

Answer 1

a.It is not a linear equation

b.L(x)=4.5 +5.7(x-1.2)

Step-by-step explanation:

Given that

`f(x)=sin 3x+x^2+5`

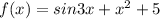
The function f(x) contains power of x more than 1 that is why it is not a linear function.This is a non-linear function.

To linearise the function

`L(x)={f(a)}'+(x-x_o)f(a)`

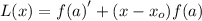
Given that

`x_o=1.2 rad` ⇒a=1.2

a=68.85°

`{f(a)}'=3 cos 3x +2x`

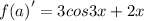
By putting the values

`{f(a)}'=3 cos 3* 68.85 +2* 1.2`

`{f(1.2)}'=4.5`

`f(1.2)=sin 3* 68.85+1.2^2+5`

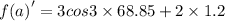
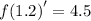
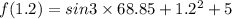
f(1.2)=5.7

`L(x)={f(a)}'+(x-x_o)f(a)`

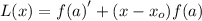
L(x)=4.5 +(x-1.2) x 5.7

L(x)=4.5 +5.7(x-1.2)