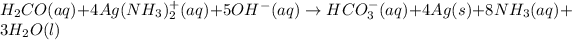Question

3. Balance each of the following redox reactions in the listed aqueous environment. (4 pts each, 8 pts total) Crs)NO3 (a) Cr (a)+NOg) (acidic) a. HCO (a)+Ags)+NH3(ag) (basic) b. H2CO(a)+Ag(NHs)2 (aq)

Answer 1

Step-by-step explanation:

(a) The given reaction equation is as follows.

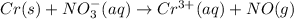`Cr(s) + NO^(-)_(3)(aq) \rightarrow Cr^(3+)(aq) + NO(g)` (acidic)

So, here the reduction and oxidation-half reactions will be as follows.

Oxidation-half reaction:
`Cr(s) \rightarrow Cr^(3+)(aq) + 3e^(-)`

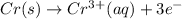
Reduction-half-reaction:
`NO^(-)_(3) + 3e^(-)(aq) \rightarrow NO(g)`

As total charge present on reactant side is -1 and total charge present on product side is +3. And, since it is present in aqueous medium. Hence, we will balance the charge for this reaction equation as follows.

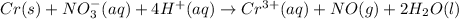`Cr(s) + NO^(-)_(3)(aq) + 4H^(+)(aq) \rightarrow Cr^(3+)(aq) + NO(g) + 2H_(2)O(l)` (acidic)

(b) The given reaction equation is as follows.

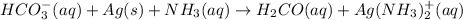`HCO^(-)_(3)(aq) + Ag(s) + NH_(3)(aq) \rightarrow H_(2)CO(aq) + Ag(NH_(3))^(+)_(2)(aq)` (basic)

So, here the reduction and oxidation-half reactions will be as follows.

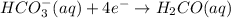
Reduction-half reaction:
`HCO^(-)_(3)(aq) + 4e^(-) \rightarrow H_(2)CO(aq)`

Oxidation-half reaction:
`Ag(s) \rightarrow Ag(NH_(3))^(+)_(2)(aq) + 1e^(-)`

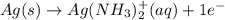
Hence, to balance the number of electrons in this equation we multiply it by 4 as follows.

`4Ag(s) \rightarrow 4Ag(NH_(3))^(+)_(2)(aq) + 4e^(-)`

Therefore, balancing the whole reaction equation in the basic medium as follows.

`H_(2)CO(aq) + 4Ag(NH_(3))^(+)_(2)(aq) + 5OH^(-)(aq) \rightarrow HCO^(-)_(3)(aq) + 4Ag(s) + 8NH_(3)(aq) + 3H_(2)O(l)`