Question

An automobile engine can produce 153 N · m of torque. Calculate the angular acceleration (in rad/s^2) produced if 85.2% of this torque is applied to the drive shaft, axle, and rear wheels of a car, given the following information. The car is suspended so that the wheels can turn freely. Each wheel acts like a 15.0 kg disk that has a 0.180 m radius. The walls of each tire act like a 2.00 kg annular ring that has inside radius of 0.180 m and outside radius of 0.320 m. The tread of each tire acts like a 10.0 kg hoop of radius 0.330 m. The 14.1 kg axle acts like a rod that has a 2.00 cm radius. The 31.7 kg drive shaft acts like a rod that has a 3.20 cm radius.

Answer 1

46.2 rad/s2

Step-by-step explanation:

Angular acceleration works very similar to linear acceleration, it follows this equation:

`\gamma = (Mt)/(J)`

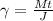
Where:

γ: angular acceleration

Mt: torque

J: moment of inertia of the load from its turning axis

Since we have the torque we just need the moment of inertia. We have to add together the moments of the drive shaft, tires, wheel walls and wheels.

The wheels act like disks. For disks the moment of inertia is:

`J = (1)/(2) * m * r^2`

`Jwheel = (1)/(2) = 15 * 0.18^2 = 0.243 kg*m^2`

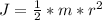
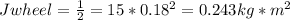
The wheel walls act like annular rings, for these the moment of inertia is:

`J = (1)/(2) * m * (re^2 - ri^2)`

`Jwall = (1)/(2) * 2 * (0.32^2 - 0.18^2) = 0.07 kg * m^2`

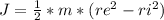
The tread acts like a hoop, as in mass concentrated into a circunference, for these:

`J = m * r^2`

`Jtread = 10 * 0.33^2 = 1.09 kg*m^2`

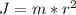
The axle acts like a rod, which is the same as the disk:

`Jaxle = (1)/(2) * 14.1 * 0.02^2 = 0.0028 kg*m^2`

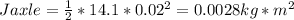
The drive shaft acts like a rod too:

`Jshaft = (1)/(2) * 31.7 * 0.032^2 = 0.016 kg*m^2`

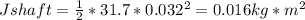
SO, the total moment of inertia is:

J = 2*Jwheel + 2*Jwall + 2*Jtread + Jaxle + Jshaft

J = 2*0.243 + 2*0.07 + 2*1.09 + 0.0028 + 0.016 = 2.82 kg*m2

Finally the angular acceleration is:

`\gamma = (0.852 * 153)/(2.82) = 46.2 (rad)/(s^2)`