Question

An air compressor of mass 120 kg is mounted on an elastic foundation. It has been observed that, when a harmonic force of amplitude 120 N is applied to the compressor, the maximum steady-state displacement of 5 mm occurred at a frequency of 320 r/min. Determine the equivalent stiffness and damping constant of the foundation.

Answer 1

equivalent stiffness is 136906.78 N/m

damping constant is 718.96 N.s/m

Step-by-step explanation:

given data

mass = 120 kg

amplitude = 120 N

frequency = 320 r/min

displacement = 5 mm

to find out

equivalent stiffness and damping

solution

we will apply here frequency formula that is

frequency ω = ω(n) √(1-∈ ²) ......................1

here ω(n) is natural frequency i.e = √(k/m)

so from equation 1

320×2π/60 = √(k/120) × √(1-2∈²)

k × ( 1 - 2∈²) = 33.51² ×120

k × ( 1 - 2∈²) = 134752.99 .....................2

and here amplitude ( max ) of displacement is express as

displacement = force / k × (
`(1)/(2\varepsilon √(1-\varepsilon ^2))`)

put here value

0.005 = 120/k × (
`(1)/(2\varepsilon √(1-\varepsilon ^2))`)

k ×∈ × √(1-2∈²) = 1200 ......................3

so by equation 3 and 2

`(k\varepsilon √(1-\varepsilon^2)))/(k(1-2\varepsilon^2)) = (12000)/(134752.99)`

`\varepsilon^(2) - \varepsilon^(4)  = 7.929 * 10^(-3) - 0.01585 * \varepsilon^(2)`

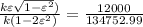
solve it and we get

∈ = 1.00396

and

∈ = 0.08869

here small value we will consider so

by equation 2 we get

k × ( 1 - 2(0.08869)²) = 134752.99

k = 136906.78 N/m

so equivalent stiffness is 136906.78 N/m

and

damping is express as

damping = 2∈ √(mk)

put here all value

damping = 2(0.08869) √(120×136906.78)

so damping constant is 718.96 N.s/m