Question

A typical home may require a total of 2.00×10^3 kWh of energy per month. Suppose you would like to obtain this energy from sunlight, which has an average daylight intensity of 1500 W/m^2 . - Assuming that sunlight is available 8.0 h per day, 25 d per month (accounting for cloudy days), and that you have a way to store energy from your collector when the Sun isn't shining, determine the smallest collector size that will provide the needed energy, given a conversion efficiency of 26 % .

Answer 1

The the smallest size of the collector is 25.64 m²

Step-by-step explanation:

Given that,

Total energy
`E=2.00*10^(3)\ kWh`

Intensity
`I= 1500 W/m^2`

Efficiency = 26%

The intensity of light can be transformed to the required energy = Available intensity of light

`I=1500*(26)/(100)`

`I=390\ W/m^2`

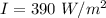
We need to calculate the smallest size of the collector

Using formula of energy related to the intensity through area and time

`E=IA\Delta t`

`A=(E)/(I\Delta t)`

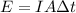
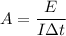
Where, E= energy

I = intensity

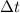`\Delta t` = time

Put the value into the formula

`A=(2.00*10^(6))/(390*25*8)`

`A=25.64\ m^2`

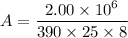
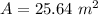
Hence, The the smallest size of the collector is 25.64 m²