Question

A 145 Ω resistor is connected in series with a 66 mH inductor and a 0.3 μF capac- itor. The applied voltage has he form E 190 V sin(2r/t), where the frequency is f 1115 cycles/s. Find the rms current Answer in units of A 005 (part 2 of 4) 10.0 points Find the ms voltage across R. Answer in units of V 006 (part 3 of 4) 10.0 points Find the ms voltage across L Answer in uts of V 007 (part 4 of 4) 10.0 points Find the rms voltage across C Answer in units of V

Answer 1

0.922 A ,133.761 volt ,426.09 volt,438.90 volt

Step-by-step explanation:

We have given resistance R=145 OHM

Inductance
`L=66 mH=66* 10^(-3)H`

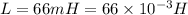
Capacitance
`C=0.3\mu F=0.3* 106{-6}F`

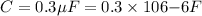
Frequency f =1115 Hz

Emf equation = 190 sin(2πft)

So rms voltage
`=(190)/(√(2))=(190)/(1.414)=134.37volt`

Inductive reactance
`X_L=\omega L=2* \pi * 1115* 66* 10^(-3)=462.1452ohm`

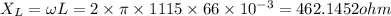
Capacitive reactance
`X_C=(1)/(\omega C)=(1)/(2* 3.14* 1115* 0.3* 10^(-6))=476.04ohm`

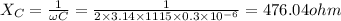
Impedance
`Z=√(R^2+(X_C-X_L)^2)=√(145^2+(476.04-462.145)^2)=145.66ohm`

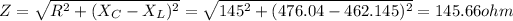
RMS current
`i=(V)/(Z)=(134.37)/(145.66)=0.922A`

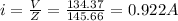
RMS voltage across resistor = 0.922×145=133.761 volt

RMS voltage across inductor =0.922×462.145=426.09 volt

RMS voltage across capacitor =0.922×438.90 volt