Question

If the first-order angle is 22.0, what can be said about the third-order angle? a. It must be within one degree of 75 b. It depends on the light wavelength, the distance of the screen from the grating, and the line spacing in the grating. c. It does't exist.

Answer 1

It depends on the light wavelength, the distance of the screen from the grating, and the line spacing in the grating.

(b) is correct option

Step-by-step explanation:

Given that,

Order number = 1

Angle = 22.0°

We need to calculate the third-order angle

Using formula of distance

`d\sin\theta=n\lambda`

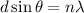
For first order,

`\sin\theta_(1)=(n\lambda)/(d)`

`\theta_(1)=\sin^(-1)(1\lambda)/(d)`

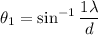
Where, d = the distance of the screen from the grating

n = order number

`\lambda`=wavelength

For second order,

`\theta_(2)=\sin^(-1)(2\lambda)/(d)`

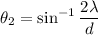
For third order,

`\theta_(3)=\sin^(-1)(3\lambda)/(d)`

So, It depends on the light wavelength, the distance of the screen from the grating, and the line spacing in the grating.

Hence, This is the required solution.