Question

a company makes a profit of $50 per software program and $35 per video game. The company can produce at most 200 software programs and at most 300 video games per week. Total production cannot exceed 435 items per week. How many items of each kind should be produced per week in order to maximize the profit? Use linear programming to solve.

Answer 1

In order to maximize the profit, should be produced 200 software program and 235 video games per week

Explanation:

Let

x ------> the number of software program

y -----> the number of video games

we know that

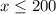`x \leq 200` -----> inequality A

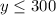`y \leq 300` -----> inequality B

`x+y \leq 435` -----> inequality C

Using a graphing tool

The solution is the shaded area between the positive values fo x and y

see the attached figure

The vertices of the shaded area are

(0,0),(0,300),(135,300),(200,235),(200,0)

The profit function is equal to

`P=50x+35y`

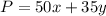
Substitute the value of x and the value of y of each vertices in the profit function

For (0,300) -----
`P=50(0)+35(300)=\$10,500`

For (135,300) -----
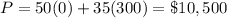
`P=50(135)+35(300)=\$17,250`

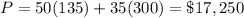
For (200,235) -----
`P=50(200)+35(235)=\$18,225`

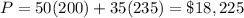
For (200,0) -----
`P=50(200)+35(0)=\$10,000`

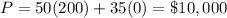
therefore

In order to maximize the profit, should be produced 200 software program and 235 video games per week