Question

What speed would a proton need to achieve in order to circle Earth 1790 km above the magnetic equator, where the Earth's mag- netic field is directed on a line between mag- netic north and south and has an intensity of 4 x 108 T? The mass of a proton is 1.673 Ã 10-21 kg

Answer 1

The velocity is 31.25 m/s and direction is toward west.

Step-by-step explanation:

Given that,

Distance
`h= 1790 km = 1.790*10^(6)\ m`

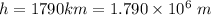
Magnetic field
`B=4*10^(-8)\ T`

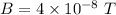
Mass of proton
`m=1.673*10^(-21)\ Kg`

Radius of earth
`R =6.38*10^(6)\ m`

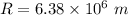
Radius of orbit
`r=R+h`

`r=6.38*10^(6)+1.790*10^(6)`

`r=8170000\ m`

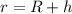
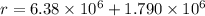
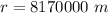
We need to calculate the speed

Using formula of magnetic field

`Bvq=(mv^2)/(r)`

`v=(Bqr)/(m)`

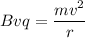
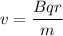
Put the value into the formula

`v=(4*10^(-8)*1.6*10^(-19)*8170000)/(1.673*10^(-21))`

`v=31.25\ m/s`

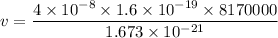
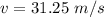
Hence, The velocity is 31.25 m/s and direction is toward west.