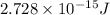Question

How much energy is released by the decay of 3 grams of 20Th in the following reaction 230 Th - 226Ra + 'He (230 Th = 229.9837 g/mol, 226Ra - 225.9771 g/mol, "He = 4.008 g/mol) (10 pts.)

Answer 1

Answer : The energy released by the decay of 3 grams of 'Th' is
`2.728* 10^(-15)J`

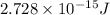
Explanation :

First we have to calculate the mass defect
`(\Delta m)`.

The balanced reaction is,

`^(230)Th\rightarrow ^(226)Ra+^(4)He`

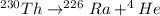
Mass defect = Sum of mass of product - sum of mass of reactants

`\Delta m=(\text{Mass of Ra}+\text{Mass of He})-(\text{Mass of Th})`

`\Delta m=(225.9771+4.008)-(229.9837)=1.4* 10^(-3)amu=2.324* 10^(-30)kg`

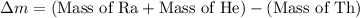
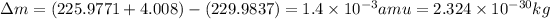
conversion used :
`(1amu=1.66* 10^(-27)kg)`

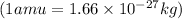
Now we have to calculate the energy released.

`Energy=\Delta m* (c)^2`

`Energy=(2.324* 10^(-30)kg)* (3* 10^8m/s)^2`

`Energy=2.0916* 10^(-13)J`

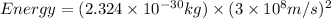
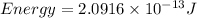
The energy released is
`2.0916* 10^(-13)J`

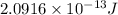
Now we have to calculate the energy released by the decay of 3 grams of 'Th'.

As, 230 grams of Th release energy =
`2.0916* 10^(-13)J`

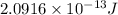
So, 3 grams of Th release energy =
`(3)/(230)* 2.0916* 10^(-13)J=2.728* 10^(-15)J`

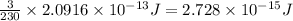
Therefore, the energy released by the decay of 3 grams of 'Th' is
`2.728* 10^(-15)J`