Question

Consider the titration of a 25 mL sample of 0.215 M KOH is titrated with 0.215 M HNO3 a. Calculate the volume of added acid that is required to reach equivalence point. (Hint: what equals what at the equivalence point?) b. The initial pH of KOH c. Calculate the pH after adding 5.0 mL of HNO,. (Hint: What kind of solution have you made? What equation can you use to calculate the pH?) d. The pH after adding 10.0, 15.0, 20.0 mL e. The pH at the equivalence point f. The pH after adding 30 mL of HNO g. Sketch the titration curve. Include labels for equivalence point, where there is excess OH and where there is excess H,O*.

Answer 1

a) 25 mL

b) 13.3

c) 13.1

d) 12.9, 12.7 and 12.3

e) 7

f) 2.97

g) The titration curve is attached, the blue line represents the curve before the equivalence point, the point in red is the equivalence point (I used excel, so I had to input at least 3 points. the equivalence point is v=25 and pH=7) and the green line represents the hydronium excess.

Step-by-step explanation:

a) At the equivalence point the moles of KOH is equal to the moles of KNO3.

`n=(C)/(v)`

Where 'n' is the number of moles, 'C' is the concentration in mol/L and 'v' is the volume in L.

At the equivalence point:

`n_(KOH) =n_(HNO3)`

Therefore:

`(C_(KOH) )/(v_(KOH))=(C_(HNO3) )/(v_(HNO3))`

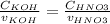
But KOH and HNO3 has the same concentration, so:

`(C )/(v_(KOH))=(C )/(v_(HNO3))`

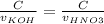
Therefore:

`v_(KOH)=v_(HNO3)`

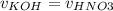
The equivalence point is when the volume of acid added is equal to the inicial volume of base, in this particular case 25 mL.

b) Before any acid is added the pH is only a function of KOH concentration.

pOH=-log[OH]

[OH-]=0.215

pOH=-log(0.215)=0.667

pH=14-pOH=13.3

pH=13.3

c) Before the equivalence point pH is given by the ammount of unreacted KOH:

Just keep in mind that the volume of acid added needs to be taken into acount

`[OH^(-) ]=(moles of KOH - moles of HNO3)/(total volume)`

`moles of KOH=(25*0.215)/(1000) =5.375x10^(-3) mol`

`moles of  HNO3=(V*0.215)/(1000) =V*2.15x10^(-4)`

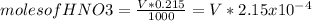
Where 'V' is the volume, in mL, of HNO3 added. Then the moles of OH- becomes:

`[OH^(-) ]=(5.375x10^(-3)- V*2.15x10^(-4))/(((25+v)/(1000) ))`

`[OH^(-) ]=(5.375x10^(-3)- 5*2.15x10^(-4))/(((25+5)/(1000) ))=0.143`

pOH=-log[OH]

[OH-]=0.143

pOH=-log(0.143)=0.844

pH=14-pOH=13.1

pH=13.1

d) Using the same formula in c) we can calculate the pH values for any volume of acid before the equivalence point.

• v=10 mL

`[OH^(-) ]=(5.375x10^(-3)- 10*2.15x10^(-4))/(((25+10)/(1000) ))=0.0921`

pH=14-pOH

pH=14-(-log(0.0921))=12.9

pH=12.9

• v=15 mL

`[OH^(-) ]=(5.375x10^(-3)- 15*2.15x10^(-4))/(((25+15)/(1000) ))=0.0538`

pH=14-pOH

pH=14-(-log(0.0538))=12.7

pH=12.7

• v=20 mL

`[OH^(-) ]=(5.375x10^(-3)- 20*2.15x10^(-4))/(((25+20)/(1000) ))=0.0239`

pH=14-pOH

pH=14-(-log(0.0239))=12.3

pH=12.3

e) This is an titration of a strong acid against a strong base, so the pH at the equivalence point is given by the autoionisation of water, so pH at equivalence point must be 7.

f) After the equivalence point the pH is given by the excess of acid.

`[H^(+) ]=((V-25)*2.15x10^(-4))/((V+25)/(1000) )`

Where 'V' is the volume, in mL, of HNO3 added.

`[H^(+) ]=((30-25)*2.15x10^(-4))/((30+25)/(1000) ) =1.075x10^(-3)`

`pH=-Log(1.075x10^(-3) )=2.97`

pH=2.97