Question

You have a quarter, mass m = 5.670 g, sliding across a table top at Subway in the Student Union. Your roommate's radar gun clocks its initial speed at vi = 3.9 m/s. The friction force on the quarter that slows it down has size 0.01 N. Calculate the stopping distance to the nearest 0.01 m. E.g., if your answer is 8.837 m, then type 8.84 in the answer box.

Answer 1

4.31 m

Step-by-step explanation:

Given:

Mass, m = 5.670 g = 5.670 × 10⁻³ kg

initial speed = 3.9 m/s

Frictional force, F = 0.01 N

Now,

the work done by the frictional force = change in the energy of the system

work done = Force × Displacement

let the stopping distance be 'x'

thus,

- Fx =
`(1)/(2)mv_f^2-(1)/(2)mv_i^2`

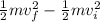
here,

negative sign means that the work done by the frictional force is in opposite direction to the movement of the mass.

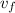`v_f` is the final speed of the mass = 0 m/s as it is stopped

therefore,

- 0.01 × x =
`(1)/(2)*5.670*0^2-(1)/(2)*5.670*3.9^2`

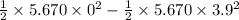
or

x = 4.31 m